Multivariate Copula Analysis Toolbox (MvCAT)
Multivariate Copula Analysis Toolbox (MvCAT), Version 1.0
Release: 12/20/2016
Source Code: Matlab
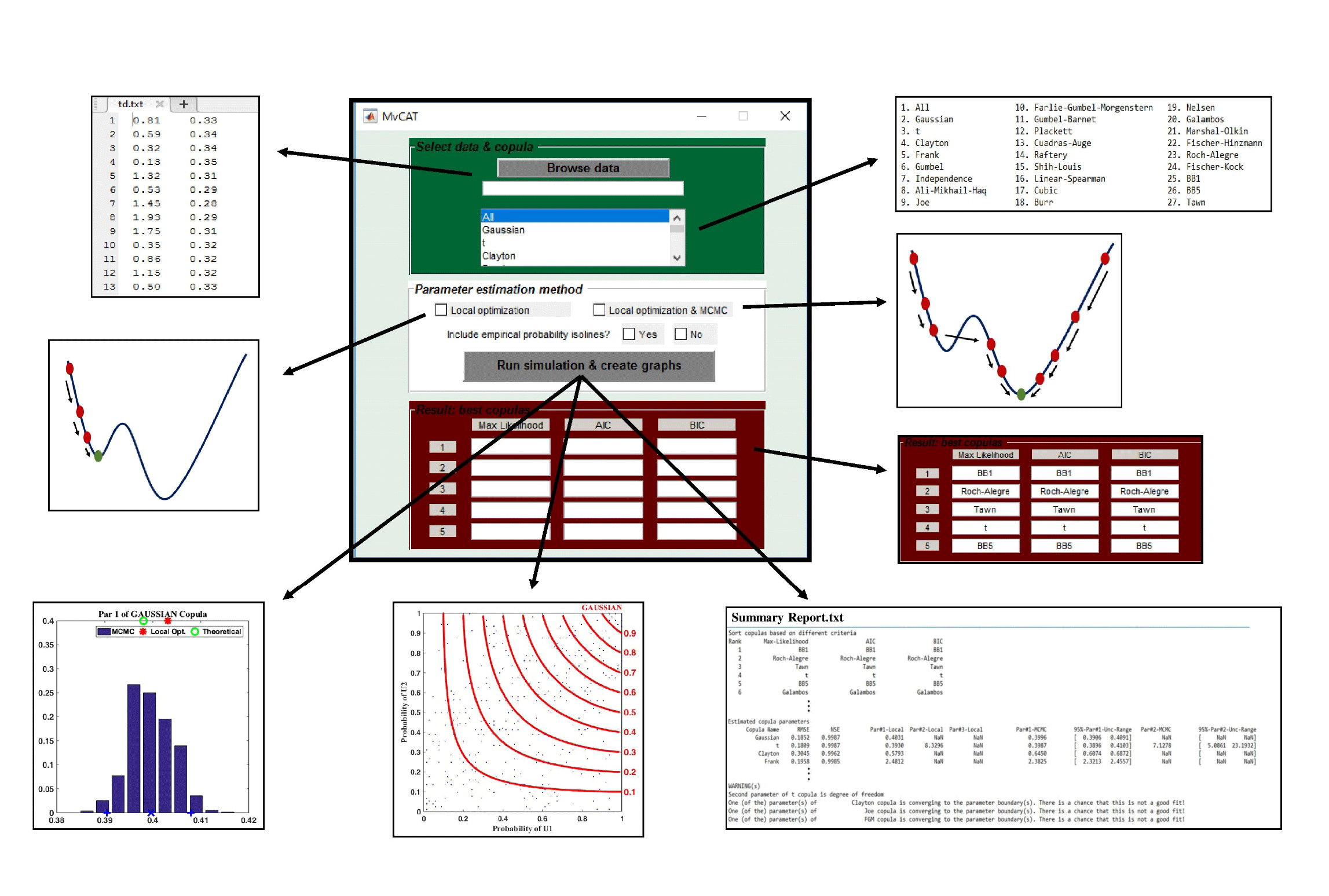
MvCAT is developed in Matlab as a user-friendly toolbox (software) to help scientists and researchers perform rigorous and comprehensive multivariate dependence analysis. It uses 26 copula families with 1 to 3 parameters to describe the dependence structure of two random variables. MvCAT uses local optimization and also Markov chain Monte Carlo simulation within a Bayesian framework to infer the parameter values of the copula families by contrasting them against available data. If Bayesian analysis with MCMC simulation is performed, an estimate of uncertainty for each copula family can be obtained from the posterior distribution of copula parameters. MCMC within Bayesian framework not only provide a robust estimate of the global optima, but also approximate the posterior distribution of the copula families which can be used to construct a prediction uncertainty range for the copulas. Local optimization methods are prone to getting trapped in local optima (see Sadegh et al., 2017 for more information). The user ca select any subset of the available 26 copulas and MvCAT will perform the analysis and rank the selected copula families based on their performance. Performance metrics used in this toolbox are Likelihood, Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), Nash-Sutcliffe Efficiency (NSE), and Root Mean Squared Error (RMSE). While Likelihood, NSE and RMSE only focus on minimizing the residuals between observations and model simulations, the other metrics take into consideration additional criteria. For example, AIC takes into account the model complexity and BIC account for model complexity and number of observations.
 |
Download Source Code
MATLAB source code of MvCAT including automatic parameter uncertainty estimation and sample input data can be retrieved from here:
Reference Publication
Sadegh M., Ragno E. and AghaKouchak A., 2017, Multivariate Copula Analysis Toolbox (MvCAT): Describing dependence and underlying uncertainty using a Bayesian framework , Water Resources Research, 53, doi:10.1002/2016WR020242. (pdf)
Sponsors








